

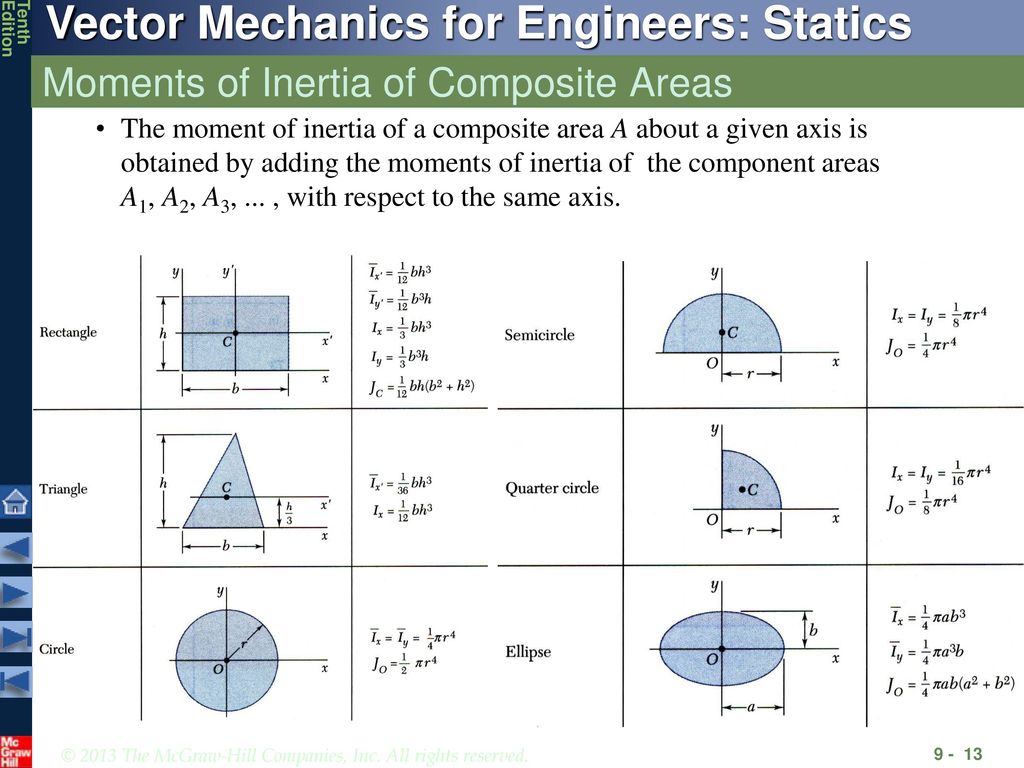
If a bar of large length when held vertically and subjected to a load at its lower end, its won-weight produces additional stress. two normal components and one shear component.ġ5. In a body loaded under plane stress conditions, what is the number of independent stress components?Įxplanation: In a body loaded under plane stress conditions, the number of independent stress components is 3 I.e. Which of these are types of normal stresses?Įxplanation: The normal stress is divided into tensile stress and compressive stress.ġ4. Normal stress is of two types tensile and compressive stress.ġ3. The stress which acts in a direction perpendicular to the area is called _Įxplanation: Normal stress acts in a direction perpendicular to the area. What will be the maximum normal stress in the column at B in the larger diameter column if the ratio of P/A here is unity?Įxplanation: Normal stress at B = Total load acting at B / Area of a cross-section at Bġ2. In the given figure a stepped column carries loads. What is the mass MOI of right circular cone of radius R and height H about its axis?Įxplanation: The mass MOI of right circular cone of radius R and height H about its axis is 3MR 2/10.ġ1. What is the mass MOI of a rectangular plate about x-axis passing through the C.G of the plate if the y-axis is parallel to d and perpendicular to b?Įxplanation: As the mass MOI is to be find along the x-axis, it would be Md 2/12.ġ0. What is mass moment of inertia of circular plate?Įxplanation: The mass moment of inertia of circular plate is Mr 2/4.ĩ. What is the unit of mass moment of inertia?Įxplanation: The mass moment of inertia is the product of moment of inertia and area. What is the product of the mass and the square of the distance of the center of gravity of the mass from an axis?Įxplanation: The product of the mass and the square of the distance of the center of gravity of the mass from an axis is known as the mass moment of inertia about that axis.ħ. and parallel to the base?Įxplanation: The moment of inertia of a triangular section about an axis passing through C.G. What is the moment of inertia of a triangular section about an axis passing through C.G.

What is the moment of inertia of a triangular section about the base?Įxplanation: The moment of inertia of a triangular section about the base is bh 3/12.ĥ. What is the moment of inertia of a rectangular section about an horizontal axis passing through base?Įxplanation: The moment of inertia of a rectangular section about an horizontal axis passing through base is bd 3/3.Ĥ. What is the moment of inertia of a rectangular section about an horizontal axis through C.G?Įxplanation: The moment of inertia of a rectangular section about an horizontal axis through C.G is bd 3/12.ģ. What is the moment of inertia of a circular section?Įxplanation: The moment of inertia of a circular section is πD 4/64.Ģ. And then if we want to find the radius of gyration we just need to take the square root of this divided by this And we get 2.1. And because it's much wider so that looks reasonable and if we had everything up we get 39.0 cubic centimeters to the fourth. Axis And this one is bigger than this one.

Because it's tall this one because it's far away from the X. And they seem reasonable because this has got a pretty high area moment about X. And we just need to add all these things up. Um And then we can calculate the area moment um about X. We can calculate the Total area of this cross section and that we get 816 cm squared.
Ix prime moment of inertia of a circle plus#
And so we have the center, we have the center the area moment about the central right? And then plus the area times this distance from the centrally to our X. And then we have the third part which is this part here. Um That's totally and so here's the values for for here. And so then we need the area of this which is B. And then we need to shift it using the parallel axis theorem from here to here. And now for two we can take the area moment about its center of mass. So the um formula for the area moment of a rectangular shape about its central void.
Axis here, which is in the center of this vertical member. So we can basically can take find the area moments for each section and then add them up to find for the total. So this part here, And then two will be this upper flank And three will be this lower flanges. So the first part, it will be the center beam here or the center section. And what we're gonna do is break it up into into three parts. So are shaded area looks something like, like what I've sketched here. Well as to determine the moment of or the second area, moment of the and the radius of gyration of the shaded area with respect to the X.


 0 kommentar(er)
0 kommentar(er)
